Джон Маккарти
Рекурсивные функции символических выражений и их вычисление машиной. Часть Ia
Дата публикации: Апрель 1960 г.
1. Введение
Система программирования LISP (LISt Processor – Обработчик списков) была разработана для компьютера IBM 704 Группой искусственного интеллекта в МТИb. Система была создана, чтобы облегчить эксперименты с гипотетической системой Advice Takerc, которая может быть запрограммирована, чтобы обрабатывать как декларативные, так и императивные выражения и демонстрировать «здравый смысл» в ходе выполнения этих программ. Первоначальный проект [1] Advice Taker был сделан в ноябре 1958 года. Основным требованием для функционирования Advice Taker было наличие системы программирования для манипуляции выражениями, представляющими формализованные декларативные и императивные высказывания, с целью обеспечения возможности дедуктивного вывода.
В ходе своего развития система LISP прошла несколько стадий упрощения и, в конечном счёте, стала основываться на схеме представления частично рекурсивных функций определённого класса символических выражений. Это представление независимо от архитектуры IBM 704 или любой другой ЭВМ. Представляется целесообразным начать описание системы с класса выражений, именуемых S-выражениями, и функций, именуемых S-функциями.
В этой статье мы вначале опишем формализм для рекурсивного определения функций. Мы верим, что этот формализм имеет преимущества и в качестве языка программирования и как средство развития теории вычислений. Далее мы опишем S-выражения и S-функции и затем универсальную S-функцию apply, которая с теоретической точки зрения может рассматриваться как универсальная машина Тьюринга, а с практической – как интерпретатор. Затем мы опишем представление S-выражений в памяти IBM 704 через списковые структуры, подобные тем, что использовали Ньювелл, Шоу и Саймон [2], и программное представление S-функций. Затем мы упомянем основных возможностей системы программирования LISP для IBM 704. Затем испробуем иной путь для описания вычислений с помощью символических выражений и, наконец, дадим блок-схему интерпретации рекурсивных функций.
Мы надеемся описать некоторые из символических вычислений, для которых LISP использовался, в других статьях, также как некоторые приложения формализма рекурсивной функции к математической логике и к проблеме автоматического доказательства теорем.
2. Функции и определения функций
Нам понадобятся некоторое количество математических идей и нотаций, касающихся функций в общем. Большинство из этих идей хорошо известны, но идея условного выражения вероятно нова1, а использование условных выражений позволяет определять функции рекурсивно новым, удобным способом.
- Частичные функции.
Частичные функции – это функции, определённые только на части своей области определения. Частичные функции закономерно возникают при определении функций через вычисления, поскольку при некоторых значениях аргументов вычисление, определяющее значение функции может быть не завершено. Однако, некоторые из наших элементарных функций будут определены в качестве частичных функций.
- Пропозициональные выражения и предикаты.
Пропозициональное выражение – это выражение, возможные значения которого T (истина) и F (ложь). Мы предполагаем, что читатель знаком с пропозициональными связками ∧ («и»), ∨ («или») и ¬ («не»). Типичными пропозициональными выражениями являются:
x < y
(x < y) ∧ (b = c)
x – простое числоПредикаты – функции, вырабатывающие значения истинности T или F.
- Условные выражения.
Связь между значениями истинности и величинами других видов выражается в математике через предикаты, а связь между значениями истинности и другими значениями истинности – через логические связки. Однако нотация для символического выражения связи величин других типов со значениями истинности неадекватна, поэтому для описания этих зависимостей обычно используются английские слова и фразы, в то время как прочие зависимости описываются символически. Например, функция |x| обычно определяется словесно. Условные выражения – это средство для выражения зависимости величин от пропозициональных величин. Условные выражения имеют форму
(p1 → e1,• • • ,pn → en), где p – пропозициональное выражение, а ¬e – выражение любого вида. Данную запись можно прочитать как «Если p1, то e1, иначе, если p2, то e2,…, иначе, если pn, то en», или как «Из p1 следует e1,…, из pn следует en»2.
Дадим теперь правила для установления, определено ли значение выражения
(p1 → e1,• • • ,pn → en), и каково это значение. Проверяем значение p слева направо. Если p со значением T вычислено перед любым p, чьё значение не определено, тогда значением условного выражения становится значение соответствующего e (если оно определено). Если какое-либо неопределённое p вычисляется до истинного p, или все p ложны, или e, соответствующее первому истинному p не определено, то значение условного выражения не определено. Приведём примеры.
(1<2→4,1>2→3)=4
(2<1→4,2>1→3,2>1→2)=3
(2<1→4,T→3)=3
(2<1→0/0,T→3)=3
(2<1→3,T→0/0) – не определено
(2<1→3,4<1→4)– не определеноНекоторые из простейших применений условных выражений даны в таких определениях как
| x| = (x < 0 → −x, T → x)
δij = (i = j → 1,T → 0)
sgn(x) = (x < 0 → −1, x = 0 → 0, T → 1) - Рекурсивное определение функций.
Используя условные выражения, мы можем без циклов определять функции с помощью формул, содержащих сами определяемые функции. Например:
n! = (n = 0 → 1,T → n • (n − 1)!) Когда мы используем эту формулу, чтобы вычислить 0!, мы получаем ответ 1, поскольку в этом случае ветка условного выражения, содержащая бессмысленное выражение 0 • (0 - 1)! не проходится. Вычисление 2! в соответствии с этим определением приводит к следующему:
2! = (2 = 0 → 1,T → 2 • (2 − 1)!)
= 2 • 1!
= 2 • (1 = 0 → 1,T →1 • (1 − 1)!)
= 2 • 1 • 0!
= 2 • 1 • (0 = 0 → 1,T → 0 • (0 − 1)!)
= 2 • 1 • 1
= 2Теперь дадим ещё два приложения рекурсивного определения функций. Наибольший общий делитель gcd(m,n) двух натуральных чисел m и n вычисляется посредством алгоритма Эвклида. Алгоритм выражается через следующее рекурсивное определение:
gcd(m,n) = (m > n → gcd(n,m),rem(n,m) = 0 → m,T → gcd(rem(n,m),m)), где rem(n,m) – остаток от деления ¬¬In на m.
Алгоритм Ньютона для приближённого вычисления квадратного корня числа a при начальном приближении x и условии остановки |y2 − a| < ε, может быть записан как
sqrt(a, x, ε) = (|x2-a|< ε→x, T →sqrt(a, ½ (x+a/x), ε)) Возможны подобные рекурсивные определения и ряда других функций; мы будем использовать их, где потребуется.
Нет гарантии, что вычисление рекурсивной функции будет когда-либо завершено. Например, вычисление ¬n! в соответствии с нашим определением будет окончено успешно только при неотрицательном целом n. Если вычисление не завершено, функция должна рассматриваться как неопределённая для данных аргументов.
Пропозициональные связки сами могут быть определены через условные выражения. Запишем
p ∧ q = (p → q,T → F)
p ∨ q = (p → T,T → q)
¬p = (p → F,T → T)
p ⊃ q = (p → q,T → T)Нетрудно убедиться в правильности таблиц истинности для правых частей уравнений. Если учесть ситуацию, когда p или q могут быть не определены, то связки ∧ и ∨ должны рассматриваться как некоммутативные. Например, если p – ложно, а q – не определено, то, в соответствии с определением, данным выше p ∧ q – ложь, но q ∧ p – не определено. Для наших целей подобная некоммутативность желательна, так как p вычисляется первым, и, в случае, если p – ложь, q не вычисляется. Если вычисление p не завершено, мы никогда не перейдём к вычислению q. Далее мы будем использовать пропозициональные связки именно в таком смысле.
- Функции и формы.
Слово «функция» в математике, за исключением математической логики, обычно используют неточно и применяют её к формам, таким как y2+x. Так как позже мы будет использовать в вычислениях выражения для функций, мы нуждаемся в разграничении функции и формы и в нотации для этого разграничения. Это разграничение и нотация для его описания, от которой мы отклонимся незначительно, даны Чёрчем [3].
Пусть f – выражение, замещающее функцию двух целых переменных. Это следует понимать в то смысле, что можно записать f(3, 4) и значение этого выражения будет определено. Выражение y2+x не удовлетворяет этому условию; y2+x(3,4) не соответствует конвенциональной нотации, и, если мы попытаемся вычислить его, мы будем не уверены, будет возвращаемый результат равен 13 или 19. Чёрч назвал выражение типа y2+x формой. Форма может быть обращена в функцию, если мы сможем определить соответствие между переменными формы и упорядоченным списком аргументов данной функции. Это достигается с помощью λ-нотации Чёрча.
Пусть ε – форма с переменными x1,• • • ,xn, тогда λ((x1,• • • , xn),ε) – функция n переменных, чьё значение определяется замещением аргументов для переменных x1,• • • ,xn в порядке, определяемым ε, с последующим вычислением полученного выражения. Например, λ((x,y),y2+x) – функция двух переменных, и λ((x,y),y2+x)(3,4)=19.
Переменные из списка переменных λ-выражения фиктивные или связанные, подобно переменным интегрирования в определённом интеграле. То есть мы можем изменять имена связанных переменных в функциональном выражении без изменения значения выражения за счёт того, что любое изменение касается каждого вхождения переменной и не объединяет переменные до этого бывшие различными. Таким образом λ((x,y),y2+x), λ((u,v),v2+u) и λ((y,x),x2+y) означает одну и ту же функцию.
Мы часто будем использовать выражения, в которых некоторые из выражений связаны λ-ой, а другие – нет. Такие выражения могут рассматриваться как определение функции с параметрами. Несвязанные переменные называются свободными переменными.
Адекватная нотация, отделяющая функцию от формы, позволяет выполнять недвусмысленное обращение функций к функциям. Пришлось бы слишком отступить от темы, чтобы привести примеры здесь, но ниже мы будем использовать функции с функциями в качестве аргументов.
Трудности возникают при комбинации функций, описанных λ-выражениями или любой другой нотацией, использующей переменные, так как различные связанные переменные могут быть представлены одинаковым символом. Это называется коллизией связанных переменных. Существует нотация, использующая операторы, называемые комбинаторами, для комбинирования функций без использования переменных. К сожалению, комбинаторные выражения для интересных комбинаций функций имеют тенденцию к большой длине и нечитаемости.
- Выражения для рекурсивных функций.
λ-нотация неадекватна для записи объявления функций, определённых рекурсивно. Например, используя её, мы можем конвертировать определение
sqrt(a,x,ε) = (|x2− a| < ε → x,T → sqrt(a, ½ (x + a/x), ε)) в
sqrt = λ((a,x,ε), |x2− a| < ε → x,T → sqrt(a, ½ (x + a/x), ε))), но правая часть уравнения не может служить выражением для функции, так как ничто не указывает на то, что ссылка на sqrt внутри выражения относится к выражению в целом.
Для того чтобы иметь возможность записывать выражения для рекурсивных функций, мы вводим другую нотацию. label(a, ε) означает то, что вхождения a в выражение ε должны быть интерпретированы как относящиеся к выражению в целом. Таким образом, мы можем записать
label(sqrt, λ((a,x,ε), |x2− a| < ε → x,T → sqrt(a, ½ (x + a/x), ε)))) в качестве объявления нашей функции sqrt.
Символ a в label(a,ε) также связан, то есть может быть изменён систематически без изменения значения выражения. Однако его поведение отличается от поведения переменной, связанной в λ.
3. Рекурсивные функции символических выражений
Вначале мы определим класс символических выражений в терминах упорядоченных пар и списков. Затем мы определим пять элементарных функций и предикатов и выстроим из них с помощью композиции, условных выражений и рекурсивных определений расширенный класс функций, к которому приведём ряд примеров. Затем мы покажем, как эти функции сами могут быть выражены в виде символических выражений и определим универсальную функцию apply, применение которой позволит нам вычислять выражение для данной функции с данными аргументами. И, наконец, мы определим несколько функций с функциями в качестве аргументов и дадим несколько полезных примеров.
- Класс символических выражений.
Определим теперь S-выражения (S – от symbolic – «символические»). Они формируются путём использования специальных знаков
•
)
(и бесконечного набора различных атомарных символов. Для атомарных символов мы будем использовать строки заглавных латинских букв и цифр с включением одиночных пробелов3. Примеры атомарных символов:
A
ABA
APPLE PIE NUMBER 3Есть две причины для отказа от обычной математической практики использования одиночных букв для атомарных символов. Во-первых, компьютерные программы часто требуют сотни различных символов, которые должны быть сформированы из 47 знаков, печатаемых компьютером IBM 704. Во-вторых, удобно использовать английские слова и фразы для обозначения атомарных сущностей по мнемоническим причинам. Символы атомарны в том смысле, что их внутренняя структура как последовательности знаков игнорируется. Она используется только для различения символов. Таким образом, S-выражения определяются следующим образом:
- Атомарные символы являются S-выражениями.
- Если e1 и e2 – S-выражения, то (e1 •e2) – также S-выражения.
Примеры S-выражений
AB
(A•B)
((AB•C) •D)S-выражение таким образом просто упорядоченная пара, термами которой могут быть атомарные символы или более простые S-выражения. Мы можем представить список произвольной длины в терминах S-выражений следующим образом. Список
(m1,m2,• • • ,mn) представляется S-выражением
(m1 • (m2 • (• • • (mn • NIL) • • •))) Здесь NIL – атомарный символ, используемый для завершения списков. Так как многие из атомарных символов, с которыми мы имеем дело, удобно выражать в виде списков, введём нотацию списка, чтобы сократить соответствующие S-выражения. Имеем:
- (m) заменяет (m • NIL).
- (m1,• • • ,mn) заменяет (m1 • (• • • (mn • NIL) • • •)).
- (m1,• • • ,mn • x) заменяет (m1 • (• • • (mn • x) • • •)).
Подвыражения можно сократить аналогичным образом. Вот примеры таких сокращений:
((AB,C),D) вместо ((AB • (C • NIL)) • (D • NIL))
((A,B),C,D • E) вместо ((A • (B • NIL)) • (C • (D • E)))Так как мы рассматриваем выражения с запятыми как сокращения выражений, не включающих запятых, отнесём их к S-выражениям.
- Функции S-выражений и выражения для их представления.
Теперь определим класс S-выражений. Выражения, представляющие эти функции, записываются в конвенционной функциональной нотации. Однако, в целях более ясного различения функций от S-выражений, для имён функций и переменных, заданных над набором S-выражений, мы будем использовать последовательности букв в нижнем регистре. Также мы используем квадратные скобки и точку с запятой вместо круглых скобок и запятых для обозначения применения функции к её аргументам. Таким образом, мы пишем
car[x]
car[cons[(A • B); x]]Любые S-выражения, появляющиеся в этих M-выражениях (мета-выражениях) означают сами себя.
- Элементарные S-функции и предикаты.
Введём следующие функции и предикаты:
- atom.
atom[x] имеет значение T или F, в зависимости от того, является ли x атомарным символом. Таким образом,
atom [X] = T
atom [(X • A)] = F - eq.
eq [x;y] определён тогда и только тогда, когда и x, и y атомарны. eq [x; y] = T, если x и y представляют собой одинаковые символы, и eq [x; y] = F в противном случае. Таким образом,
eq [X; X] = T
eq [X; A] = F
eq [X; (X • A)] – не определено. - car.
car[x] определён тогда и только тогда, когда x не атомарен. car [(e1 • e2)] = e1. Таким образом, car [X] не определён.
car [(X • A)] = X
car [((X • A) • Y )] = (X • A) - cdr.
cdr [x] также определён, когда x не атомарен. cdr[(e1 • e2)] = e2. Таким образом, cdr [X] не определён
cdr [(X • A)] = A
cdr [((X • A) • Y )] = Y - cons.
cons [x; y] определён для любого x и y. cons [e1; e2] = (e1 • e2). Таким образом
cons [X; A] = (X A)
cons [(X • A); Y ] = ((X • A)Y )
Как нетрудно увидеть, car, cdr, и cons удовлетворяют отношениям
car [cons [x; y]] = x
cdr [cons [x; y]] = y
cons [car [x]; cdr [x]] = x, предполагая, что x не атомарен.Имена «car» и «cons» будут иметь мнемоническое значение только при обсуждении представления системы на компьютере. Сочетания car и cdr даёт подвыражения данного выражения на заданной позиции. Сочетания cons формирует выражения заданной структуры из отдельных частей. Класс функций, формируемых этими способами, довольно ограничен и не особо интересен.
- atom.
- Рекурсивные S-функции.
Мы получим намного больший класс функций (фактически все вычислимые функции), если допустим формирование новых функций S-выражений с помощью условных выражений и рекурсивного определения. Вот несколько примеров функций, определяемых данным способом.
- ff[x].
Значением ff[x] является первый атомарный символ S-выражения x, игнорируя скобки. Таким образом
ff[((A • B) • C)] = A Имеем:
ff[x] = [atom[x] → x; T → ff[car[x]]] Рассмотрим детально шаги выполнения ff [((A • B) • C)]:
ff [((A • B) • C)]
= [atom[((A • B) • C)] → ((A • B) • C); T → ff[car[((A • B)C• )]]]
= [F → ((A • B) • C); T → ff[car[((A • B) • C)]]]
= [T → ff[car[((A • B) • C)]]]
= ff[car[((A • B) • C)]
= ff[(A • B)]
= [atom[(A • B)] → (A • B); T → ff[car[(A • B)]]]
= [F → (A • B); T → ff[car[(A • B)]]]
= [T → ff[car[(A • B)]]]
= ff[car[(A • B)]]
= ff[A]
= [atom[A] → A; T → ff[car[A]]]
= [T → A; T → ff[car[A]]]
= A - subst [x; y; z].
Эта функция заменяет все вхождения атомарного символа y в S-выражении z на S-выражение x. Определение:
subst [x;y;z] = [atom [z] → [eq [z; y] → x; T → z];
T → cons [subst [x; y; car [z]]; subst [x; y; cdr [z]]]]Приведём пример:
subst[(X • A); B; ((A • B) • C)] = ((A • (X • A)) • C) - equal [x;y].
Этот предикат имеет значение T, если x и y являются одинаковыми S-выражениями, и значение F в противном случае. Имеем:
equal [x;y] = [atom [x] ∧ atom [y] ∧ eq [x; y]]
∨[¬ atom [x] ∧¬ atom [y] ∧ equal [car [x]; car [y]]
∧ equal [cdr [x]; cdr [y]]]
Полезно посмотреть, как элементарные функции выглядят в сокращённой списочной нотации. Читатель легко убедится, что
(i) car[(m1,m2,• • • ,mn)] = m1
(ii) cdr[(m1,m2,• • • ,mn)] = (m2,• • • ,mn)
(iii) cdr[(m)] = NIL
(iv) cons[m1; (m2,• • • ,mn)] = (m1,m2,• • • ,mn)
(v) cons[m; NIL] = (m)Пусть
null[x] = atom[x] ∧ eq[x; NIL] Этот предикат полезен при работе со списками.
Сочетание car и cdr встречается так часто, что многие выражения можно записать более кратко, если принять сокращение:
cadr[x] для car[cdr[x]],
caddr[x] для car[cdr[cdr[x]]] и т.д.Другое полезное сокращение – запись list [e1; e2; • • •; en] вместо cons[e1; cons[e2; • • •; cons[en; NIL] • • •]].
Эта функция даёт список (e1,• • • ,en) как функцию его элементов.
Следующие функции полезны для S-выражений, рассматриваемых как списки.
- append [x; y].
append [x; y] = [null[x] → y; T → cons [car [x]; append [cdr [x]; y]]] Пример:
append [(A, B); (C, D, E)] = (A, B, C, D, E) - among[x; y].
Этот предикат истинен, если S-выражение x входит в число элементов списка y. Имеем:
among[x; y] = ¬null[y] ∧ [equal[x; car[y]] ∨ among[x; cdr[y]]] - pair[x; y].
Эта функция даётe список пар соответствующих элементов списков x и y. Имеем:
pair[x; y] = [null[x]∧null[y] → NIL; ¬atom[x]∧¬atom[y] → cons[list[car[x]; car[y]]; pair[cdr[x]; cdr[y]]] Пример:
pair[(A,B,C); (X,(Y,Z),U)] = ((A,X),(B,(Y,Z)),(C,U)). - assoc[x; y].
Если y – список вида ((u1,v1),• • • ,(un,vn)), а x – один из u, тогда значение assoc [x; y] – соответствующий v. Имеем:
assoc[x; y] = eq[caar[y]; x] → cadar[y]; T → assoc[x; cdr[y]]] Пример:
assoc[X; ((W,(A,B)),(X,(C,D)),(Y,(E,F)))] = (C,D). - sublis[x; y].
Здесь предполагается, что x имеет форму списка пар ((u1,v1),• • • ,(un,vn)), где все u – атомы, а y может быть любым S-выражением. Значение sublis[x;y] – результат замены в выражении y каждого v на соответствующий u. Для того чтобы определить sublis, определим вначале вспомогательную функцию:
sub2[x; z] = [null[x] → z; eq[caar[x]; z] → cadar[x]; T → sub2[cdr[x]; z]] И далее:
sublis[x; y] = [atom[y] → sub2[x; y]; T → cons[sublis[x; car[y]]; sublis[x; cdr[y]]] Например:
sublis [((X, (A, B)), (Y, (B, C))); (A, X • Y)] = (A, (A, B), B, C)
- ff[x].
- Представление S-функций посредством S-выражений.
Мы описали S-функции с помощью M-выражений. Дадим сейчас правило для трансляции M-выражений в S-выражения для того, чтобы сделать возможными для S-функций ряд вычислений и для ответа на ряд вопросов о S-функциях.
Трансляция ε* M-выражения ε определяется следующими правилами:
- Если ε – S-выражение, то ε* = (QUOTE, ε).
- Переменные и имена функций, представленные строками букв в нижнем регистре транслируются в соответствующие строки соответствующих заглавных букв. Так car* = CAR, а subst* = SUBST.
- Форма f[e1; • • •; en] транслируется в f[e1*, • • • , en*] . Так cons [car [x];cdr [x]]* = (CONS, (CAR, X), (CDR, X)).
- {[p1 → e1; • • • ; pn → en]}* = (COND, (p1*,e1*),…,(pn*,en*)).
- {λ[[x1; • • • ; xn]; ε]}* = (LAMBDA, (x1*,…,xn*), ε*).
- {label[a; ε]} = (LABEL, a*, ε*).
С использованием этих конвенций замена таких функциональных M-выражений как [subst; λ [[x; y; z]; [atom [z] → [eq [y; z] → x; T → z]; T → cons [subst[x; y; car [z]]; subst [x; y; cdr [z]]]]]] даст следующие S-выражения:
(LABEL, SUBST, (LAMBDA, (X, Y, Z), (COND ((ATOM, Z), (COND,(EQ, Y, Z), X), ((QUOTE, T), Z))), ((QUOTE, T), (CONS, (SUBST, X, Y,(CAR Z)), (SUBST, X, Y, (CDR, Z)))))))
Эту нотацию можно записать и отчасти даже прочитать. Можно облегчить чтение и запись ценой уменьшения регулярности структуры. Если бы большее количество символов было доступно на компьютере, это серьёзно бы улучшило положение4.
- Универсальная S-функция apply.
S-функция apply обладает следующим свойством: если f – S-выражение для S-функции f ' , а args –список аргументов формы (arg1,• • • ,argn), где arg1,• • • ,argn – произвольные S-выражения, тогда apply[f; args] и f ' [arg1; • • • ; argn] определены для одинаковых значений arg1; • • • ; argn и равны, когда определены. Например:
λ[[x; y]; cons[car[x]; y]][(A,B); (C,D)] =
apply[(LAMBDA,(X,Y ),(CONS,(CAR,X),Y)); ((A,B),(C,D))] = (A,C,D)S-функция apply определяется как
apply[f; args] = eval[cons[f; appq[args]]; NIL], где
appq[m] = [null[m] → NIL; T → cons[list[QUOTE; car[m]]; appq[cdr[m]]]], а
eval[e; a] = [
atom [e] → assoc [e; a];
atom [car [e]] → [
eq [car [e]; QUOTE] → cadr [e];
eq [car [e]; ATOM] → atom [eval [cadr [e]; a]];
eq [car [e]; EQ] → [eval [cadr [e]; a] = eval [caddr [e]; a]];
eq [car [e]; COND] → evcon [cdr [e]; a];
eq [car [e]; CAR] → car [eval [cadr [e]; a]];
eq [car [e]; CDR] → cdr [eval [cadr [e]; a]];
eq [car [e]; CONS] → cons [eval [cadr [e]; a]; eval [caddr [e];
a]]; T → eval [cons [assoc [car [e]; a];
evlis [cdr [e]; a]]; a]];
eq [caar [e]; LABEL] → eval [cons [caddar [e]; cdr [e]];
cons [list [cadar [e]; car [e]; a]];
eq [caar [e]; LAMBDA] → eval [caddar [e];
append [pair [cadar [e]; evlis [cdr [e]; a]; a]]],и
evcon[c; a] = [eval[caar[c]; a] → eval[cadar[c]; a]; T → evcon[cdr[c]; a],], и
evlis[m; a] = [null[m] → NIL; T → cons[eval[car[m]; a]; evlis[cdr[m]; a]]]. Разъясним некоторые детали этих определений5.
- Сам apply формирует выражение, выдающее значение функции, применённой к аргументам, и возлагает работу по вычислению этого выражения на функцию eval. Она использует appq для добавления QUOTE к каждому аргументу, чтобы eval обращался к ним, как они есть.
- eval[e; a] имеет два аргумента – выражение e, которое должно быть вычислено и список пар a. Первый член каждой пары – атомарный символ, а второй – выражение, обозначаемое этим символом.
- Если выражение, которое должно быть вычислено, атомарно, eval вычисляет первое парное этому атому выражение из списка a.
- Если e не атомарно, но car[e] – атомарно, тогда выражение имеет одну из форм: (QUOTE,e), или (ATOM,e), или (EQ,e1,e2), или (COND,(p1,e1),• • • ,(pn,en)), или (CAR,e), или (CDR,e), или (CONS,e1,e2), или (f,e1,• • • ,en), где f – атомарный символ.
В случае (QUOTE,e) берётся выражение e само по себе. В случае (ATOM,e), или (CAR,e), или (CDR,e) выражение e вычисляется и берётся соответствующая функция. В случае (EQ,e1,e2) или (CONS,e1,e2) должны быть вычислены два выражения. В случае (COND,(p1,e1),• • • (pn,en)) значения p вычисляются по порядку до тех пор, пока не будет найдено истинное p, после чего должно быть вычислено соответствующее e. Это выполняется с помощью evcon. Наконец, в случае (f,e1,• • • ,en) мы вычисляем выражение, полученное путём замены f в этом выражении соответствующей парой из списка a. - Вычисление ((LABEL,f,ε),e1,• • • ,en) производится путём вычисления (ε ,e1,• • • ,en) с парой (f,(LABEL,f, ε)), поставленной перед предшествующим списком пар.
- 6. Наконец, вычисление ((LAMBDA,(x1,• • • ,xn), ε),e1,• • • en) производится путём вычисления ε ((x1,e1),• • • ,((xn,en)), поставленным перед предшествующим списком a.
Список a может быть удалён, а выражения LAMBDA и LABEL будут вычисляться подстановкой аргументов для переменных в выражении ε. К сожалению, при этом возникают трудности с разрешением коллизий со связанными переменными, но они устраняются использованием списка a.
Вычисление значений функций с использованием apply – деятельность, к которой лучше приспособлены электронные компьютеры, а не люди. Однако сейчас мы в качестве иллюстрации покажем несколько шагов вычисления
apply [(LABEL, FF, (LAMBDA, (X), (COND, (ATOM, X), X), ((QUOTE,T),(FF, (CAR, X))))));((A• B))] = A Первый аргумент – S-выражение, которое представляет функцию ff, определённую в разделе 3-d. Обозначим её буквой φ. Имеем
apply [φ; ( (A• B) )]
= eval [((LABEL, FF, ψ), (QUOTE, (A• B))); NIL],где ψ – часть φ, начинающаяся с (LAMBDA
= eval[((LAMBDA, (X), ω), (QUOTE, (A• B)));((FF, φ))], где ω – часть ψ, начинающаяся с (COND
= eval [(COND, (π1,ε1),(π2, ε2)); ((X, (QUOTE, (A• B) ) ), (FF, φ) )] Обозначая ((X, (QUOTE, (A• B))), (FF, φ)) через a, получаем
= evcon [((π1,ε1),(π2, ε2)); a] Отсюда следует
eval [π1; a]
= eval [( ATOM, X); a]
= atom [eval [X; a]]
= atom [eval [assoc [X; ((X, (QUOTE, (A• B))), (FF,φ))];a]]
= atom [eval [(QUOTE, (A• B)); a]]
= atom [(A• B)],
= FПроцесс вычисления продолжится с
apply [φ; ((A• B))]
= evcon [((π2, ε2,)); a],отсюда
eval [π2; a] = eval [(QUOTE, T); a] = T Вновь продолжаем
apply [φ; ((A• B))]
= eval [ε2; a]
= eval [(FF, (CAR, X));a]
= eval [Cons [φ; evlis [((CAR, X)); a]]; a]Вычисляя evlis [((CAR, X)); a] получаем
eval [(CAR, X); a]
= car [eval [X; a]]
= car [(A• B)], где мы берём шаги из более раннего вычисления
atom [eval [X; a]] = A,и, таким образом, evlis [((CAR, X)); a] даёт
list [list [QUOTE; A]] = ((QUOTE, A)), и отсюда получаем
= eval [(φ, (QUOTE, A)); a] Последующие шаги производятся аналогично началу вычисления. LABEL и LAMBDA добавляют новые пары к a, что формирует новый список пар a1. Терм π1 условного выражения eval [(ATOM, X); a1] имеет значение T, поскольку X спарен с (QUOTE, A) в a1 ранее, чем (QUOTE, (A• B)) как в a.
Следовательно, мы заканчиваем с eval [X; a1] из evcon, что даёт A
- Функции с функциями в качестве аргументов.
Есть некоторое количество полезных функций, некоторые из аргументов которых являются функциями. Они особенно полезны при определении других функций. Одна из таких функций maplist[x;f] имеет два аргумента – S-выражение x и аргумент f – функцию, преобразовывающую S-выражения в S-выражения. Дадим определение:
maplist[x;f] = [null[x] →NIL;T→cons[f[x];maplist[cdr[x];f]]] Полезность maplist иллюстрируется формулами частного производного относительно x выражений, включающих суммы и произведения x с другими переменными. S-выражения, которые мы будем дифференцировать формируются следующим образом.
- Атомарный символ является разрешённым выражением.
- Если e1, e2,…, en – разрешённые выражения, то (PLUS, e1,…, en) и (TIMES, e1,…, en) также разрешены и представляют собой, соответственно, сумму и произведение e1,…, en.
Это, по сути, польская нотация для функций, не считая включения скобок и запятых, что позволяет использовать функции переменного числа аргументов. Пример разрешённой функции (TIMES, X,(PLUS, X,A), Y), что в стандартной алгебраической нотации даёт X(X+ A)Y.
Частная производная y относительно x вычисляется по формуле
diff [y; x] = [atom [y]→[eq [y; x] →ONE; T→ZERO]; eq [car [Y]; PLUS]→cons [PLUS; maplist [cdr [y];λ[[z]; diff [car [z]; x]]]]; eq[car [y]; TIMES] →cons[PLUS; maplist[cdr[y];λ[[z]; cons [TIMES; maplist[cdr [y]; λ[[w]; ¬eq [z;w]→car [w]; T→diff [car [[w]; x]]]]]] Производная выражения (TIMES, X, (PLUS, X, A), Y), вычисленная согласно данной формуле:
(PLUS, (TIMES, ONE, (PLUS, X, A), Y), (TIMES, X, (PLUS, ONE,ZERO), Y), (TIMES, X, (PLUS, X, A), ZERO)) Помимо maplist другой полезной функцией с функциональными аргументами является search, определяемая как
search[x;p;f;u] = [null[x] →u;p[x] →f[x];T→search[cdr[x];p;f;u] Функция search используется для поиска в списке элемента, обладающего свойством p, и, если такой элемент найден, берётся f от данного элемента. Если такого элемента нет, вычисляется функция u, не имеющая аргументов.
4. Система программирования LISP
Система программирования LISP создана для использования компьютера IBM 704 для вычисления символической информации в форме S-выражений. Она используется или будет использоваться для следующих целей:
- Написания компилятора для компиляции программ на LISP в машинный язык.
- Написания программы для проведения проверок в классе формальных логических систем.
- Написания программ для формального дифференцирования и интегрирования.
- Написания программ для реализации различных алгоритмов генерации проверок в исчислении предикатов.
- Проведения некоторых инженерных вычислений с результатами, выраженными формулами, а не числами.
- Программирования системы Advice Taker.
Основа системы – технология написания компьютерных программ для исполнения S-функций. Она будет описана в последующих разделах.
Дополнительно к возможностям описания S-функций, существуют возможности использования S-функций в программах, записанных в виде последовательностей команд наподобие FORTRAN [4] или ALGOL [5]. В данной статье эти возможности не рассматриваются.
- Представление S-выражений через списковую структуру.
Списковая структура – коллекция компьютерных слов, упорядоченная, как показано на рисунке 1a или 1b. Каждое слово списковой структуры представлено одним из разделённых пополам прямоугольников на рисунке. Левая ячейка прямоугольника представляет адресное поле слова, а правая ячейка – декрементное поле. Стрелка от ячейки к другому прямоугольнику означает, что поле, соответствующее ячейке, содержит адрес слова, соответствующего другому прямоугольнику.
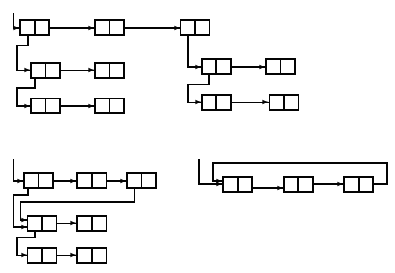
Рисунок 1 Допустимо, чтобы отдельные субструктуры появлялись более чем в одном месте списковой структуры, как на рисунке 1b, но не допустимы циклы в составе структуры, как на рисунке 1c. Атомарный символ представлен в компьютере списковой структурой специальной формы, называемой ассоциированный список символа. Адресное поле первого слова содержит специальную константу, которая позволяет программе определить, что это слово представляет атомарный символ. Мы опишем ассоциированный список в разделе 4b.
S-выражение x, не являющееся атомарным, представлено словом, адресная и декрементная часть которого содержат адреса подвыражений car[x] и cdr[x], соответственно. Если мы используем символы A, B и т.д., чтобы обозначить адреса ассоциированных списков этих символов, то S-выражение ((A•B)• (C• (E•F))) будет представлено списковой структурой a рисунка 2. А S-выражение (A,(B,C),D), являющееся сокращением для (A•((B•(C•NIL))•(D•NIL))), представлено списковой структурой рисунка 2b.
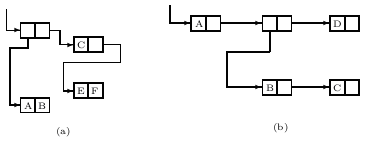
Рисунок 2 Когда списковая структура используется для представления списка, каждый терм списка занимает адресную часть слова, декрементная часть которого указывает на слово, содержащее следующий терм, в то время как последнее слово содержит NIL в своём декременте.
Выражение, имеющее подвыражения, возникающее более одного раза, может быть представлено более чем одним способом. Будет ли списковая структура для подвыражения повторена или нет, зависит от истории программы. Повторяется или нет подвыражение, не имеет значения для выдачи результатов программой, хотя это может повлиять на требования к времени исполнения и к памяти. Например, S-выражение ((A•B)•(A•B)) может быть представлено способами, показанными на рисунке 3a или 3b.
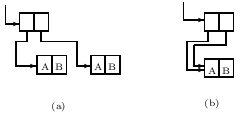
Рисунок 3 Запрет на циклические списковые структуры есть, по сути, запрет на выражения, являющиеся подвыражениями самого себя. Такое выражение не может существовать на бумаге в мире с нашей топологией. Циклические списковые структуры могли бы иметь некоторые преимущества для компьютера, например для представления рекурсивных функций, однако трудности с их распечаткой и рядом других операций делают нежелательными их использование в настоящем.
Использование списковых структур для хранения символических выражений имеет следующие преимущества:
- Размер и даже количество выражений, с которыми программа будет вынуждена работать, невозможно предсказать заранее. Поэтому сложно разметить блоки хранения фиксированной длины для их приёма.
- Регистры могут быть возвращены в список свободной памяти, если они больше не нужны. Возвращение даже одного регистра в список полезно, однако при линейной организации памяти трудно организовать повторное использование блоков регистров произвольного размера.
- Выражение, являющееся подвыражением нескольких выражений, может быть представлено в памяти в одиночном экземпляре.
- Ассоциированные списки6.
В ассоциированные списки символов LISPа мы заложили больше, чем требовалось математической системой, описанной в предыдущих разделах. Фактически, любую информацию, которую мы желаем ассоциировать с символом, можно занести в ассоциированный список. Эта информация может включать: имя для печати, то есть строку букв и цифр, которая представляет символ для восприятия человеком; числовое значение, если символ представляет число, другое S-выражение, если символ каким-либо образом служит именем для него; или адрес процедуры, если символ представляет функцию, для которой существует подпрограмма на машинном языке. Всё это подразумевает, что машинная система включает больше примитивных сущностей, чем было описано в разделах по математической системе.
Сейчас мы опишем только, как в ассоциированном списке представляется имя для печати, для того чтобы обеспечить соответствие между информацией на перфокартах, магнитной ленте или печатной странице и списковой структурой внутри машины. Ассоциированный список символа DIFFERENTIATE имеет сегмент формы, показанной на рисунке 4. Здесь pname – символ, который указывает, что структура, содержащая имя для печати символа, начинается со следующего слова ассоциированного списка. Во втором ряду рисунка мы видим список из трёх слов. Адресная часть каждого из этих слов указывает на слово, содержащее шесть 6-битных знаков. Последнее слово заполнено 6-битными комбинациями, не представляющими знаков, выводимых на печать компьютером. (Напоминаем, что IBM 7O4 использует 36-битное слово, и каждый знак, выводимый на печать, представлен 6 битами). Присутствие слов с символьной информацией означает, что ассоциируемые списки сами по себе не представляют S-выражения, и только некоторые из функций для работы с S-выражениями имеют смысл в рамках ассоциированного списка.
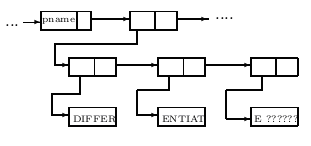
Рисунок 4 - Список свободной памяти.
В любой момент времени только часть памяти, зарезервированной для списковых структур, будет реально использоваться для хранения S-выражений. Остающиеся регистры (в нашей системе их, изначально, около 15 000) заносятся в простой список, называемый списком свободной памяти. Определённый регистр (FREE) в программе содержит адрес первого регистра в этом списке. Когда требуется слово для формирования некоторой дополнительной списковой структуры, берётся первое слово из списка свободной памяти, а число в регистре FREE меняется на адрес второго слова в списке свободной памяти. Пользователю не нужды заботиться о программировании возврата регистров в список свободной памяти.
Этот возврат осуществляется автоматически примерно следующим образом (в данной статье мы сочли нужным дать упрощённое описание процесса): В программе существует фиксированный набор базовых регистров, которые содержат адреса списковых структур, доступных программе. Конечно, так как списковые структуры ветвятся, может быть вовлечено неопределённое количество регистров. Каждый регистр, доступный программе, доступен потому, что его можно достигнуть из одного или более базовых регистров по цепочке операций car и cdr. Если содержимое базового регистра меняется, может случиться так, что регистр, на который данный базовый регистр ранее указывал, больше не может быть достигнут по цепочке car−cdr ни с одного базового регистра. Такой регистр можно рассматривать как неиспользуемый программой, так как его содержимое больше не может быть найдено ни одним возможным способом; следовательно, его содержимое больше не представляет интереса, и желательно вернуть его в список свободной памяти. Это происходит следующим образом.
Пока программа не нуждается в дополнительной памяти, ничего не происходит. Когда требуется свободный регистр, а в списке свободной памяти ничего не осталось, запускается цикл утилизации7.
Вначале программа находит все регистры, доступные из базовых регистров, и делает их знаки отрицательными. Для этого она стартует из каждого базового регистра и меняет знак всех регистров, которые могут быть достигнуты по цепочке car−cdr. Если программе в ходе этого процесса встречается регистр, знак которого уже отрицателен, это означает, что данный регистр уже был достигнут.
После того, как знаки у всех доступных регистров были изменены, программа просматривает область памяти, зарезервированную для хранения списковых структур, возвращает все регистры, чьи знаки не были изменены на предыдущем шаге, обратно в список свободной памяти и делает знаки всех доступных регистров вновь положительными.
Этот процесс, так как он полностью автоматический, удобнее для программиста, чем система, в которой он должен отслеживать и стирать ненужные списки. Его эффективность зависит от недопущения исчерпания памяти доступной для поддержки списков. Процесс утилизации требует нескольких секунд, и поэтому, чтобы программа не тратила большую часть своего времени на утилизацию, должен возвращать в список свободной памяти не меньше нескольких тысяч регистров.
- Элементарные S-функции в компьютере.
Опишем теперь компьютерное представление atom, = , car, cdr и cons. S-выражения связаны с программами, которые рассматривают функции как адреса слов, представляющих их, и выдают результаты в такой же форме.
atom. Как было указано выше, слово, представляющее атомарный символ, содержит специальную константу в своей адресной части: atom запрограммирован как открытая подпрограмма, тестирующая эту часть. Если только M-выражение atom[e] не выступает как условие в условном выражении, то в результате этого теста генерируются символы T или F. В случае условного выражения используется условный перенос, а символы T или F не генерируются.
eq. Программа для eq[e;f] тестирует адреса слов на числовое равенство. Это работает потому, что каждый атомарный символ имеет только один ассоциированный список. Как и в случае с atom, результатом является либо условный перенос, либо один из символов T или F.
car. Вычисление car[x] представляет собой взятие содержимого адресной части регистра x. По сути это достигается применением одиночной инструкции CLA 0, i, аргумент для которой берётся из индексного регистра, а результат заносится в адресную часть аккумулятора. (Мы предполагаем, что места, из которых функция берёт свои аргументы, и в которые она кладёт результаты, прописаны в определении функции, и на программисте или на компиляторе лежит ответственность по вставке требуемых инструкций по перемещению данных, чтобы передать результат одного вычисления в позицию для следующего). («car» – мнемоник для «contents of the address part of register» – «содержимое адресной части регистра»).
cdr. cdr обрабатывается также, как car, за исключением того, что результат заносится в декрементную часть аккумулятора («cdr» заменяет «contents of the decrement part of register» – «содержимое декрементной части регистра»).
cons. Значением cons[x;y] должен быть адрес регистра, имеющего x и y в своей адресной и декрементной частях соответственно. В компьютере может не быть такого регистра, и, даже если он есть, было бы слишком времязатратно его искать. Что мы делаем реально, это берём первый доступный регистр из списка свободной памяти, помещаем x и y в адресную и декрементную части соответственно и делаем значением функции адрес взятого регистра. («cons» – сокращение для «construct» – «составить»).
Для cons есть подпрограмма, начинающая утилизацию, если список свободной памяти исчерпан. В той версии системы, что используется в настоящее время, cons представлен закрытой подпрограммой. В скомпилированной версии cons открыт.
- Представление S-функций программами.
Компиляция функций-композиций car, cdr, и cons, вручную или программой-компилятором, тривиальна. Условные выражения также не вызывают затруднений, за исключением того, что их следует компилировать таким образом, чтобы только требуемые p и e вычислялись. Однако проблемы возникают при компиляции рекурсивных функций.
Вообще (позже мы рассмотрим исключение), программа для рекурсивной функции использует себя в качестве подпрограммы. Например, программа для subst[x;y;z] использует себя в качестве подпрограммы, чтобы вычислить результат подстановки в подвыражениях car[z] и cdr[z]. Пока вычисляется subst[x;y;cdr[z]], результат предыдущего вычисления subst[x;y;car[z]] следует сохранить в регистре временного хранения. Однако subst может нуждаться в этом же регистре для вычисления subst[x;y;cdr[z]]. Возможный конфликт разрешается программами SAVE и UNSAVE, которые используют общий магазинный список8. Программа SAVE входит в начало программы для рекурсивной функции с запросом на сохранения данного набора последовательных регистров. Для этой цели резервируется блок регистров, называемый общий магазинный список. Программе SAVE доступен индекс, говорящий, сколько регистров в магазинном списке уже используются. Она перемещает содержимое регистров, которые должны быть сохранены в первые неиспользуемые регистры магазинного списка, увеличивает индекс списка и возвращает контроль программе. Эта программа может теперь свободно использовать данные регистры для временного хранения. Перед завершением программа использует UNSAVE, которая восстанавливает содержимое временных регистров из магазинного списка и откатывает индекс этого списка. Результатом этих соглашений является то, что, говоря программистским языком, рекурсивная подпрограмма прозрачна по отношению к регистрам временного хранения.
- Состояние системы программирования LISP (февраль 1960 г.).
Вариант функции apply, описанной в разделе 5-f, был транслирован в программу APPLY для IBM 704. Так как эта программа может вычислять значения S-функций, заданных их описаниями в виде S-выражений и их аргументами, она служит интерпретатором языка программирования LISP, который описывает вычислительные процессы именно таким образом.
Программа APPLY встроена в систему программирования LISP, которая имеет следующие возможности:
- Программист может определить с помощью S-выражений любое количество S-функций. Эти функции могут связываться друг с другом или с какими-либо S-функциями, представленными программами на машинном языке.
- Значения определённых функций могут быть вычислены.
- S-выражения могут быть прочитаны и напечатаны (напрямую или через магнитную ленту).
- Включены некоторые возможности по диагностике ошибок и выборочной трассировке.
- Программист может записать выбранные S-функции, скомпилированные в машинный код, в постоянную память. Значения скомпилированных функций вычисляются примерно в 60 раз быстрее, чем при интерпретации. Компиляция протекает достаточно быстро, так что нет необходимости заготавливать скомпилированные программы про запас.
- «Программная опция» позволяет запускать программы с присвоением и оператором go to в стиле ALGOL.
- В системе возможны, но непроизводительны вычисления с плавающей точкой.
- Готовится руководство программиста. Система программирования LISP наиболее подходит для вычислений, где данные удобно представлять в виде символических выражений, в том числе включающих подвыражения. Версия системы для IBM 709 в процессе разработки.
5. Другой формализм для функций символических выражений
Существует ряд способов определения функций символических выражений, близких к принятой нами системе. Каждый из них включает три базовых функции, условные выражения и определения рекурсивных функций, но отличается классом выражений, соответствующих S-выражениям, и, следовательно, точными определениями функций. Опишем один из таких вариантов, называемый линейным LISP.
L-выражения определяются следующим образом:
- Устанавливается конечный список символов.
- Любая строка допустимых символов является L-выражением, включая пустую строку, обозначаемую Λ.
Существуют три строковые функции:
- first[x] – первый символ строки x. first[Λ] не определён. Например: first[ABC] = A.
- rest[x] – строка символов, которая остаётся после удаления первого символа строки. rest[Λ] не определён. Например: rest[ABC] = BC.
- combine[x;y] – строка, получаемая постановкой символа x в начало строки y. Например: combine[A;BC] = ABC.
Существует три строковых предиката:
- char[x], x – одиночный символ.
- null[x], x – пустая строка.
- x=y, определён для символов x и y.
Преимущество линейного LISP в отсутствии символов, играющих специальные роли, таких как скобки, точки и запятые в LISP. Это позволяет выполнять вычисления со всеми выражениями, которые могут быть записаны линейно. Недостаток линейного LISP в том, что извлечение подвыражений представляет собой довольно запутанную, неэлементарную операцию. В рамках линейного LISP нетрудно написать функции, соответствующие базовым функциям LISP, таким образом математически линейный LISP включает в себя LISP. Линейный LISP более удобен для программирования сложных манипуляций. Однако, при исполнении на компьютере LISP существенно быстрее.
6. Блок-схемы и рекурсия
Так как и обычная форма компьютерных программ и определения рекурсивных функций оба универсально вычислимы, интересно показать связь между ними. Трансляция рекурсивных символических функций в компьютерные программы была предметом предыдущей части статьи. В этом разделе мы покажем другой путь, по крайней мере в принципе.
Состояние машины в любой момент времени во время вычисления задаётся значениями набора переменных. Пусть эти переменные объединены в вектор ξ. Рассмотрим программный блок с одним входом и одним выходом. Он определяет и, по существу, определяется функцией f, которая переводит одну машинную конфигурацию в другую, то есть имеет форму ξ ' = f(ξ). Назовём f ассоциированной функцией программного блока. Теперь пусть некоторое количество таких блоков будет объединено в программу с помощью элементов π, принимающих решение о том, какой блок будет исполняться следующим, когда текущий блок завершится. Тем не менее, пусть программа в целом по-прежнему имеет один вход и один выход.
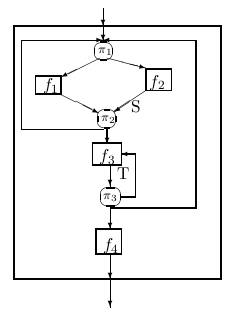 |
| Рисунок 5 |
В качестве примера дадим блок-схему на рисунке 5. Опишем функцию r[ξ], которая трансформирует вектор ξ между входом и выходом всего блока. Определим её как объединение функций s(ξ) и t[ξ], которые производят трансформации ξ между точками S и T, соответственно, и выходом. Имеем
S[ξ] = [π21[ξ] →r[ξ];T→t[f3[ξ]]]
t[ξ] = [π31[ξ] →f4[ξ];π32[ξ] →r[ξ];T→t[f3[ξ]]]
С помощью блок-схемы с одиночными входом и выходом легко записывать рекурсивные функции, производящие трансформацию вектора состояния от входа к выходу, в терминах соответствующих функций для вычислительных блоков и предикатов ветвления. Обобщённо представим это следующим образом.
На рисунке 6 пусть β будет n-валентной точкой ветвления, а f1,…,fn – вычислениями, ведущими к точкам ветвления β1,β2,…,βn. Пусть φ – функция, трансформирующая ξ между β и выходом из диаграммы, а φ1,…,φn – соответствующие функции для β1,…,βn. Запишем
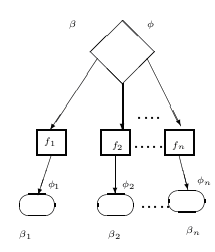 |
| Рисунок 6 |
7. Благодарности
Неадекватность λ-нотации для именования рекурсивных функций была отмечена N. Rochester, также он открыл альтернативу с label, которая используется здесь. Вариант подпрограммы для cons, допускающий её композицию с другими функциями, был создан, также и для других систем программирования, C. Gerberick и H. L. Gelernter, IBM Corporation. Система программирования LlSP была разработана группой, включающей R. Brayton, D. Edwards, P. Fox, L. Hodes, D. Luckham, K. Maling, J. McCarthy (Дж. Маккарти), D. Park, S. Russell.
Поддержку группе оказывал Вычислительный центр МТИ и Исследовательская лаборатория электроники МТИ (которую поддерживают в частности Армия США (войска связи), Военно-воздушные силы США (Управление научных исследований, воздушных исследований и группа развития) и Военно-морской флот США (Управление военно-морских исследований)). Автор также хотел бы выразить благодарность за личную финансовую поддержку Фонд Альфреда П. Слоана.
Литература
- J. McCARTHY, Programs with common sense, Paper presented at the Symposium on the Mechanization of Thought Processes, National Physical Laboratory, Teddington, England, Nov. 24-27, 1958. (Published in Proceedings of the Symposium by H. M. Stationery Office).
- NEWELL AND J. C. SHAW, Programming the logic theory machine, Proc. Western Joint Computer Conference, Feb. 1957.
- CHURCH, The Calculi of Lambda-Conversion (Princeton University Press, Princeton, N. J., 1941).
- FORTRAN Programmer’s Reference Manual, IBM Corporation, New York, Oct. 15, 1956.
- J. PERLIS AND K. SAMELS0N, International algebraic language, Preliminary Report, Comm. Assoc. Comp. Mach., Dec. 1958.
Примечания автора:
- См. Kleened.
- Я направил предложение по поводу включения условных выражений в Алгол 60 в журнал CACM (Communication of the ACM). Поскольку предложение было коротким, редактор разжаловал его до письма в редакцию, за что CACM впоследствии извинился. Представленная здесь нотация была отвергнута составителями Алгол 60, так как было решено не использовать в Алгол 60 новые математические нотации, а всё новое выражать на английском. Конструкция if . . . then . . . else, принятая в Алгол 60 была предложена Джоном Бэкусом .
- Примечание 1995 года: пробелы внутри символов были допустимы, поскольку списки тогда писали с запятыми между элементамиe.
- Примечание 1995 года: больше символов было добавлено в SAILf и, позже, на Лисп-машинах. Увы, мир вернулся к худшему набору символов, хотя и не настолько плохому, который был, когда эта статья была написана в начале 1959 г.
- Примечание 1995 года: Эта версия не совсем правильна. Сравнение данной и других версий eval, включая ту, что была на самом деле реализована (и отлажена) дано в «The Influence of the Designer on the Design» Герберта Стояна и включена в Artificial Intelligence and Mathematical Theory of Computation: Papers in Honor of John McCarthy, Vladimir Lifschitz (ed.), Academic Press, 1991.
- Примечание 1995 года: позже он были названы списками свойств.
- Мы уже называли этот процесс «сборка мусора», но я предпочёл отказаться от его использования в этой статье – иначе грамматические дамы из Исследовательской лаборатории электроники её бы не пропустили.
- Примечание 1995 г.: теперь называемый стекомg.
Примечания переводчика:
- Части II не существует.
- МТИ – Массачусетский технологический институт.
- Advice Taker – гипотетическая программа, описанная Джоном Маккарти в 1958 г. в статье «Programs with Common Sense». Считается первой в мире полной системой искусственного интеллекта.
- Стивен Коул Клейни (Клини) – американский математик, один из основоположников теории рекурсии.
- В современном Лиспе пробелы используются для разделения атомов.
- SAIL – Stanford Artificial Intellect Laboratory – Стэнфордская лаборатория искусственного интеллекта.
- Магазинный – в смысле с проталкиванием вниз, как в оружейном магазине.